Answer:
The equation of the line is 5y-3x=0.
Step-by-step explanation:
We are given two points: (x1,y1)=(5, 3) and (x2,y2)=(-5, -3)
Thus, we use the two-point form below to find the equation of the line.
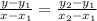
Substituting the points gives:
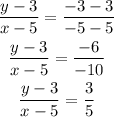
Next, simplify:
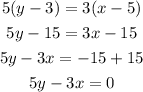
The equation of the line is 5y-3x=0.