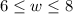Question

If I want to buy an area rug for my room. I would like the rug to be no smaller than 48 square feet and no bigger than 80 square feet. If the length is 2 feet more than the width, what are the range of possible values for the width.

Answer 1

Given that:

- The rug should be no smaller than 48 square feet and no bigger than 80 square feet.

- The length is 2 feet more than the width.

The formula for calculating the area of a rectangle is:

`A=lw`

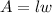
Where "l" is the length and "w" is the width.

In this case, you know that:

`l=w+2`

Therefore, you can express the formula for the area of the rectangular rug as:

`A=(w+2)w`

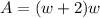
Now you can set up the following inequality:

`48\leq(w+2)w\leq80`

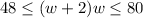
Solve for "w", in order to find the range of possible values for the width:

1. Apply the Distributive Property:

`48\leq(w)(w)+(2)(w)\leq80`
`48\leq w^2+2w\leq80`

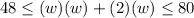
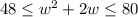
2. Set up the first inequality:

`48\leq w^2+2w\text{ }`

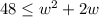
Subtract 48 from both sides:

`48-48\leq w^2+2w-48`
`0\leq w^2+2w-48\text{ }`

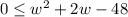
Factor it and solve for "w":

`\begin{gathered} 0\leq(w-6)(w+8) \\ \\ 6\leq w \\ -8\leq w \end{gathered}`

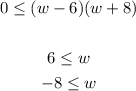
3. Set up the second inequality and apply the same procedure:

`w^2+2w\leq80`
`\begin{gathered} w^2+2w-80\leq0 \\ (w-8)(w+10)\leq0 \\ w\leq8 \\ w\leq-10 \end{gathered}`

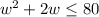
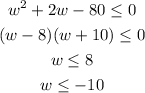
The width must be positive.

Hence, the answer is:

`6\leq w\leq8`