Question

please help! functions and relations. f(x)= square root of x-4. find the inverse of f(x) and it’s domain.

Answer 1

`\:D.\text{ }f^(-1)\left(x\right)=\left(x+4\right)^2;x\ge-4`

Explanation:

We have the following equation:

`f(x)=√(x)-4`

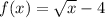
The inverse is the following (we calculate it by replacing f(x) by x and x by f(x)):

`\begin{gathered} x=\sqrt{f^(-1)(x)}-4 \\ \\ \sqrt{f^(-1)(x)}=x+4 \\ \\ f^(-1)(x)=(x+4)^2 \end{gathered}`

The domain would be the range of the original equation, and it would be the range of values that f(x) could take, which was from -4 to positive infinity, that is, f(x) ≥ -4.

Therefore, the domain is x ≥ -4.

So the correct answer is D.

`\:f^(-1)\left(x\right)=\left(x+4\right)^2;x\ge -4`