Question

What is the domain and range of ƒ(x)=√7-x^2

Answer 1

The function given is

`f(x)=√(7-x^2)`

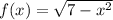
The domain of a function is the set of input values (x-values) for which the function is defined or real.

To obtain the domain of the function above, we need to solve the expression in the square root.

`\begin{gathered} 7-x^2\ge0 \\ \text{Then, subtract 7 from both sides} \\ 7-7-x^2\ge0-7 \\ -x^2\ge-7 \\ \text{Multiply both sides by -1} \\ x^2\le7 \end{gathered}`

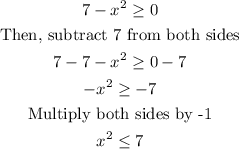
Take square root of both sides we have

`\begin{gathered} √(x^2)\le\pm\sqrt[]{7} \\ \text{Then} \\ x^{}\le\pm\sqrt[]{7} \end{gathered}`

Hence, the domain becomes

`\begin{gathered} -√(7)\le\: x\le√(7) \\ or \\ \mleft[-√(7),\: √(7)\mright] \end{gathered}`

Domain is [-√7,√7]

Similarly, for th range of f(x) we have

`\begin{gathered} \mleft[0,\: √(7)\mright] \\ or \\ \: 0\le\: f\mleft(x\mright)\le√(7) \end{gathered}`

Therefore

Range is [0,√7]