As given by the question
There are given that the system of the equation:
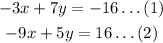
Now,
From the equation (1):
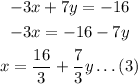
Put the value of equation (3) into equation (2)
So,
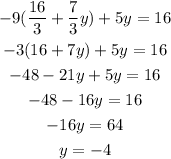
Then,
Put the value of y into the equation (3)
So,
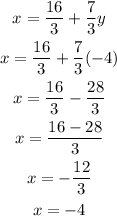
Hence, the value of x is -4 and the value of y is -4.