We are given that an airplane travelling at 160 km/h and 160 meters high will drop supplies. The problem can be exemplified in the following diagram:
Due to inertia, the movement of the supplies will be that of a parabolic motion. therefore, we can use the following equation of motion:
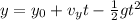
Where:

Since the plane travels horizontally, this means that the vertical velocity of the object is zero, therefore, we have:

The value of the height "y" is zero since we want to determine the time when the object hits the ground, therefore we have:
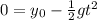
Now we solve for the time "t" first by subtracting the initial height from both sides:
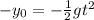
Now we multiply both sides by -2:
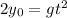
Now we divide both sides by "g":
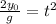
Now we take the square root to both sides:
![\sqrt[]{(2y_0)/(g)}=t](https://img.qammunity.org/2023/formulas/physics/college/x0e9bfmjyfhtdmjnpgagtsjqg6fbsprarp.png)
Replacing the given values we get:
![\sqrt[]{(2(160m))/(9.8(m)/(s^2))}=t](https://img.qammunity.org/2023/formulas/physics/college/w8oc8wdxrnm6enrcjzqjpwnfolaesvatpy.png)
Solving the operations we get:
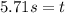
Therefore, the supplies must be dropped 5.71s before the plane is directly overhead.