Question

Find the value(s) of k that will cause the equation to have the given number and type of solutions.6x² + kx + 6 +0, 1 real solution

Answer 1

`6x^2+kx+6=0`

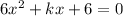
we can use the equation to factor

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a=6 , b=k and c=6

replacing

`\begin{gathered} x=\frac{-k\pm\sqrt[]{k^2-4(6)(6)}}{2(6)} \\ \\ x=\frac{-k\pm\sqrt[]{k^2-4(6)(6)}}{2(6)} \\ \\ x=\frac{-k\pm\sqrt[]{k^2-144}}{12} \end{gathered}`

to have a real solution we need the interior of the root to be greater than or equal to 0

so

`\begin{gathered} k^2-144\ge0 \\ k^2\ge144 \\ k\ge\pm\sqrt[]{144} \\ k\le-12ork\ge12 \end{gathered}`

The solution is option B

k can take any value in the interval K<-12 or in the interval k>12