Solution
- The general form of a sinusoidal function is:

- First of all, let us find the value of B using the period formula given above.
![\begin{gathered} \text{ We are told that the period is 6} \\ \therefore T=(2\pi)/(|B|) \\ \\ 6=(2\pi)/(|B|) \\ \text{ Make \mid B\mid the subject of the formula} \\ \\ \therefore|B|=(2\pi)/(6) \\ \\ |B|=(\pi)/(3) \\ \\ \text{ Thus,} \\ B=\pm(\pi)/(3) \\ \\ \text{ Since there is only the positive }(\pi)/(3)\text{ in the options,} \\ \\ B=(\pi)/(3) \end{gathered}]()
- Next, we should apply the condition given to us that f(2.5) = 5
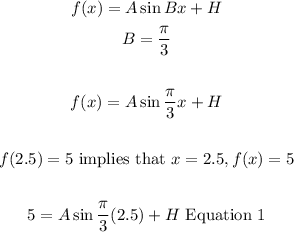
- We also know that the Amplitude and Valley are related to the midline as follows:

Solving equations 1 and 2 simultaneously, we have