Question

Simplify (-64)3/2 ? Hint: Not a real number.

Answer 1

We want to simplify

`(-64)^{(3)/(2)}`

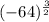
When we exponentiate a number by a fraction, we exponentiate the number by the numerator, and the denominator is the radical of the root. Since our denominator is 2, we have a square root.

`(-64)^{(3)/(2)}=\sqrt[]{(-64)^3}`

Expanding this expression, we have

`\begin{gathered} \sqrt[]{(-64)^3}=\sqrt[]{(-1)^3(64)^3} \\ =\sqrt[]{(-1)^{}(64)^2(64)} \\ =64\sqrt[]{(-1)(64)} \\ =64\sqrt[]{(-1)(8)^2} \\ =64\cdot8\sqrt[]{(-1)^{}} \\ =512\sqrt[]{-1^{}} \end{gathered}`

The square root of minus one is also know as the imaginary number.

`512\sqrt[]{-1^{}}=512i`