Hello!
Let's write some important information contained in the exercise:
Were sold 800 tickets
• cheap + expensive = 800
The price of each ticket was:
• cheap: SEK 90
,
• expensive: SEK 120
The total ticket revenue was SEK 85,500.
Note: let's use 'c' for cheap and 'e' for expensive.
Knowing it, we can write it as a linear system look:
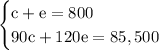
Let's rewrite the first equation as:
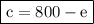
Now, let's replace the value of c in the second equation:

Now that we know the number of expensive tickets sold, let's find the number of cheap tickets using equation 1 again:
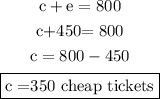
Answer:
There were sold:
• 350 cheap tickets.
,
• 450 expensive tickets.