Question

(square root)7 - x = x + 5. Find x

Answer 1

.We have the following equation,

`\sqrt[]{7-x}=x+5`

First, we can note that the term into the radical must be zero or positive, that is,

`\begin{gathered} 7-x\ge0 \\ \text{which means} \\ x\le7 \end{gathered}`

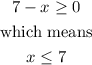
Then, by squaring both sides, we have

`\begin{gathered} 7-x=(x+5)^2 \\ or\text{ equivalently,} \\ 7-x=x^2+10x+25 \end{gathered}`

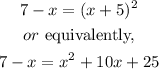
Now, by subtracting 7 to both sides, we have

`-x=x^2+10x+18`

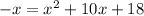
and by adding x to both sides, we get

`\begin{gathered} 0=x^2+11x+18 \\ or\text{ equivalently,} \\ x^2+11x+18=0 \end{gathered}`

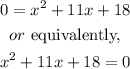
Now, we can use the quadratic formula, that is,

`x=\frac{-11\pm\sqrt[]{11^2-4(1)(18)}}{2}`

which gives

`\begin{gathered} x=\frac{-11\pm\sqrt[]{121-72}}{2} \\ x=\frac{-11\pm\sqrt[]{49}}{2} \\ x=(-11\pm7)/(2) \end{gathered}`

then, the solutions are

`\begin{gathered} x=(-4)/(2)=-2 \\ \text{and} \\ x=(-18)/(2)=-9 \end{gathered}`

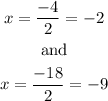
Now, we know that an extraneous solution is a solution that does not work. Then, by substituting x=-9 into the given equation, we have

`\sqrt[]{7-(-9)}=-9+5`

which gives

`\begin{gathered} \sqrt[]{7+9}=-4 \\ \sqrt[]{16}=-4 \\ 4=-4 \end{gathered}`

which is an absurd result. Then, x=-9 is an extraneous solution.

On the other hand, by substituting x=-2, we obtain

`\begin{gathered} \sqrt[]{7-(-2)}=-2+5 \\ \sqrt[]{7+2}=3 \\ \sqrt[]{9}=3 \\ 3=3 \end{gathered}`

which is correct.

Therefore, the answers are:

`\begin{gathered} \text{Extraneous solution: x=-9} \\ \text{True solution: x=-2} \end{gathered}`