Solution:
Given:
Two transversals with four line segments.
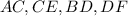
Part A:
For the line segment AC, the length is the distance between points A and C.
![\begin{gathered} A=(5,7) \\ C=(6,4) \\ \text{where;} \\ x_1=5,y_1=7 \\ x_2=6,y_2=4 \\ \\ \text{The distance betwe}en\text{ two points is given by;} \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ \text{Hence,} \\ d=\sqrt[]{(6-5)^2+(4-7)^2} \\ d=\sqrt[]{1^2+(-3)^2} \\ d=\sqrt[]{1+9} \\ d=\sqrt[]{10} \\ To\text{ the nearest hundredth,} \\ d_(AC)\approx3.16 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nsmigy28tkis7eoc7h5k4ghchc4ew8eih8.png)
For the line segment CE, the length is the distance between points C and E.
![\begin{gathered} C=(6,4) \\ E=(7,1) \\ \text{where;} \\ x_1=6,y_1=4 \\ x_2=7,y_2=1 \\ \\ \text{The distance betwe}en\text{ two points is given by;} \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ \text{Hence,} \\ d=\sqrt[]{(7-6)^2+(1-4)^2} \\ d=\sqrt[]{1^2+(-3)^2} \\ d=\sqrt[]{1+9} \\ d=\sqrt[]{10} \\ To\text{ the nearest hundredth,} \\ d_(CE)\approx3.16 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pfrf6mkokmojb4ymjlbcquwuyxx27nmpd6.png)
For the line segment BD, the length is the distance between points B and D.
![\begin{gathered} B=(17,7) \\ D=(16,4) \\ \text{where;} \\ x_1=17,y_1=7 \\ x_2=16,y_2=4 \\ \\ \text{The distance betwe}en\text{ two points is given by;} \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ \text{Hence,} \\ d=\sqrt[]{(16-17)^2+(4-7)^2} \\ d=\sqrt[]{(-1)^2+(-3)^2} \\ d=\sqrt[]{1+9} \\ d=\sqrt[]{10} \\ To\text{ the nearest hundredth,} \\ d_(BD)\approx3.16 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r6062zb5qpvbcoi7e9oigyhq4y4742acw8.png)
For the line segment DF, the length is the distance between points D and F.
![\begin{gathered} D=(16,4) \\ F=(15,1) \\ \text{where;} \\ x_1=16,y_1=4 \\ x_2=15,y_2=1 \\ \\ \text{The distance betwe}en\text{ two points is given by;} \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ \text{Hence,} \\ d=\sqrt[]{(15-16)^2+(1-4)^2} \\ d=\sqrt[]{(-1)^2+(-3)^2} \\ d=\sqrt[]{1+9} \\ d_{}=\sqrt[]{10} \\ To\text{ the nearest hundredth,} \\ d_(DF)\approx3.16 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k1vbpl2h2s2es8m2wj80f4t72mqhnnuvk1.png)
Part B:
On the first transversal, the ratio of the lengths of the line segments formed on it is;
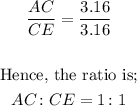
On the second transversal, the ratio of the lengths of the line segments formed on it is;
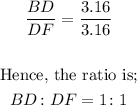
From the ratio of the lengths of each transversal, it is noticed that they are the same.