Question

Find the equation of the exponential function represented by the table below:

т
y
0
4
12
36
108

Answer 1

We have a table that represents an exponential function.

We can express an exponential function as:

`y=a\cdot b^x`

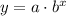
We can use the values of the table to calculate the parameters "a" and "b".

For example we can use the value of y when x = 0 to calculate "a":

`\begin{gathered} y(0)=4 \\ a\cdot b^0=4 \\ a\cdot1=4 \\ a=4 \end{gathered}`

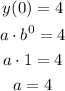
We then can use two consecutive values to find the parameter "b":

`\begin{gathered} (y(2))/(y(1))=(a\cdot b^2)/(a\cdot b^1)=b^(2-1)=b \\ \Rightarrow b=(y(2))/(y(1))=(36)/(12)=3 \end{gathered}`

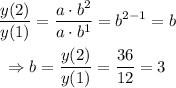
Then, we can express the exponential function as:

`y=4\cdot3^x`

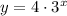
Answer: y = 4*3^x