Question

Determine, to the nearest tenth, the perimeter of the triangle shown in the accompanying diagram.

Answer 1

D. 23.3

Explanation:

The perimeter of a triangle is the sum of all its side lengths,

Given the coordinates of the vertices of triangle ABC as:

• A(-9,6), B(-3,10) and C(-2,2)

First, we find the side lengths using the distance formula below:

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

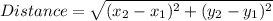
Using points A(-9,6) and B(-3,10):

`\begin{gathered} AB=\sqrt[]{(-3-(-9))^2+(10-6)^2} \\ =\sqrt[]{(-3+9)^2+(4)^2}=\sqrt[]{(6)^2+(4)^2}=\sqrt[]{36+16} \\ AB=\sqrt[]{52} \end{gathered}`

Using points B(-3,10) and C(-2,2):

`\begin{gathered} BC=\sqrt[]{(-2-(-3))^2+(2-10)^2} \\ =\sqrt[]{(-2+3)^2+(-8)^2}=\sqrt[]{(1)^2+(-8)^2}=\sqrt[]{1+64} \\ BC=\sqrt[]{65} \end{gathered}`

Finally, using points A(-9,6) and C(-2,2):

`\begin{gathered} AC=\sqrt[]{(-2-(-9))^2+(2-6)^2} \\ =\sqrt[]{(-2+9)^2+(-4)^2}=\sqrt[]{(7)^2+(-4)^2}=\sqrt[]{49+16} \\ AC=\sqrt[]{65} \end{gathered}`

Therefore, the perimeter of triangle ABC is:

`\begin{gathered} \text{Perimeter}=AB+BC+AC \\ =\sqrt[]{52}+\sqrt[]{65}+\sqrt[]{65} \\ =23.3\text{ units} \end{gathered}`

The correct option is D.