ANSWER
43.5 square units
Step-by-step explanation
Given that this is not a right triangle, the easier method to obtain its area is to find the area of the rectangle where the triangle's vertices are on three of the four sides of the rectangle,
The area of triangle ABC is the area of the rectangle, minus the areas of the three right triangles shaded in red.
The dimensions of the rectangle are 15 units wide by 9 units long, so the area is,

The area of each triangle is found with the formula,
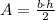
The height of triangle 1 is 9 units, while its base is 8 units long,
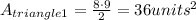
The height of triangle 2 is 3 units, and the base is 7 units,
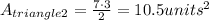
The height of triangle 3 is 6 units and its base is 15 units,

So the area of triangle ABC is,
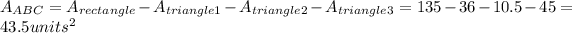
Hence, the area of triangle ABC is 43.5 square units.