Answer:
x = 76 / 9 [ 8 (4 / 9) =
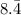 ]
]
y = 68 / 9 [ 7 (5 / 9) =
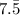 ]
]
__________________
Explanation:
There are several methods that can be used to solve systems but in this situation, it is generally easier to cancel out a variable by adding the system of equations together.
This is how it's done:
x + y = 16
5x – 4y = 12
__________
4 ( x + y = 16 )
+ 5x – 4y = 12
[Multiplying the entire equation by 4 to cancel out the y because 4y – 4y = 0]
___________
4x + 4y = 64
+ 5x – 4y = 12
__________
9x = 76
÷9 ÷9
[Dividing by the coefficient of 9x in x to get x]
______
x = 76 / 9.
_______
Now that we have the x variable, you can simply substitute that quantity into x + y = 16 to solve for y.
So:
x + y = 16
[substituting the value of x into the equation]
(76 / 9) + y = 16
[Creating a common denominator that
can be canceled out]
(76 / 9) + (9y / 9) = (144 / 9)
76 + 9y = 144
[Subtracting 76 from both sides to isolate 9y]
–76 –76
__________
9y = 68
÷9 ÷9
[Dividing both sides by the coefficient of 9y in y to get y]
_________
y = 68 / 9
_________
We can also verify that these variables have the correct value because:
x + y = 16
5x – 4y = 12
→
(76 / 9) + (68 / 9) = 16
5(76 / 9) – 4(68 / 9) = 12
__________________
(76 + 68 / 9) = 16
(380 / 9) – (272 / 9) = 12
___________________
144 / 9 = 16
(380 – 272 / 9) = 12
__________________
144 / 9 × 9 = 16 × 9
108 / 9 = 12
__________________
144 = 144 ✓
108 / 9 × 9 = 12 × 9
_________________
144 = 144 ✓
108 = 108 ✓