Question

For every 3 minivans in a school parking, lot there are five cars. If there are a total of 96 minivans and cars in parking lot, how many of the vehicles are minivans and how many are cars?

Answer 1

Let x be the number of vans and y the number of cars.

We are told that for every 3 vans we get 5 car. This translates to the equation

`y\text{ = }(5)/(3)x`

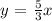
Note that if we replace x=3, we get y=5 which is what we are told.

Now, we have 96 vehicles in total, so

`x+y\text{ = 96}`

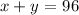
Now, we replace the value of y with what we found in the first equation, so

`x\text{ + }(5)/(3)x\text{ = 96 = }(8)/(3)x`

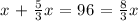
If we multiply by 3 on both sides, we get

`8x\text{ = 96}\cdot3\text{ = 288 }`

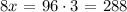
If we now divide by 8 we get

`x\text{ = }(288)/(8)\text{ = 36}`

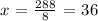
Since x+y = 96 and x = 36, then we must have y = 60.

So, there are 36 vans and 60 cars