The formula for the distance is given by:
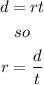
- So, the rate of the airplane against the wind is:
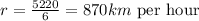
- The rate of the airplane with the wind is:
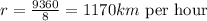
- Next, the rate of the wind is given by:

- And finally, the rate of the plane and still air is:
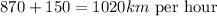
Answer:
the rate of the plane and still air = 1020 km per hour
the rate of the wind = 150 km per hour