We will determine the domain of the function as follows:
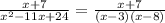
So, the domain is the following:
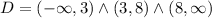
**Explanation***
In order to determine the domain of the function, we factor the denominator and evaluate at which points the denominator will become zero. [When this happens the function is not defined and thus those values do not belong in the domain].
When we factor the denominator, we obtain:
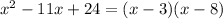
So, we equal the factor to zero and find which points do not belong in the domain:
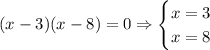
So, the equation "makes sense" in all of the real numbers, except when x = 3 and x = 8.