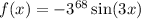Question

Find this function after differentiating it 68 times:f(x) = sin (3x)

Answer 1

Given the function:

`f(x)=\sin (3x)`

Let's find the function after differentiating it 68 times.

To differentiate, let's take the derivative.

First derivative:

`\begin{gathered} f\text{'(x)= cos(}3x)(d)/(dx)(3x)_{} \\ \\ f^(\prime)(x)=3\cos (3x) \end{gathered}`

Second derivative:

Since 3 is the constant with respect to x, the derivative of 3cos(3x) with respect to x will be:

`\begin{gathered} f^(\doubleprime)(x)=3(d)/(dx)(\cos (3x)) \\ \\ f^(\doubleprime)(x)=3(-\sin (3x)(d)/(dx)(3x)) \\ \\ f^(\doubleprime)(x)=-3\sin (3x)(3(d)/(dx)(x)) \\ \\ f^(\doubleprime)(x)=-9\sin (3x)(d)/(dx)(x) \\ \\ f^(\doubleprime)(x)=-3^2\sin (3x) \end{gathered}`

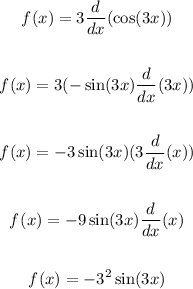
After the second differentiation, we have -sin, , the same will be applicable to the 68th time.

Therefore, for the 68th differentiation the exponent for the constant -3 will be 68.

`f(x)=-3^(68)\sin (3x)`

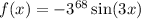
Therefore, after differentiating the function 68 times, we have:

`f(x)=-3^(68)\sin (3x)`

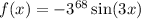
ANSWER:

`f(x)=-3^(68)\sin (3x)`