Hello!
We have the following expression:

We can solve it as a geometric sequence, I'll show you how.
First, let's write the number of terms of the sequence:
Starting in 0 until 6, we have: a1, a2, a3, a4, a5, a6 and a7.
(7 terms).
Also, we can see that the ratio is 1.05.
Now, let's calculate the first term of the sequence (a1):
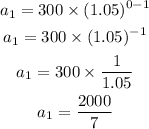
As we know the first term of the sequence and the ratio, we can use the formula below to calculate the sum of the 7 terms of this sequence:
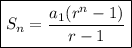
So, let's replace it with the values that we already know:
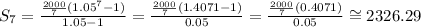
Right answer: alternative B.