Given:
Principal amount = $5000
Interest rate = 16%
Find-:
(a) Amount owed at the end of 1 year.
(b) Amount owed at the end of 1 year.
Sol:
The compound interest rate is:

Where,
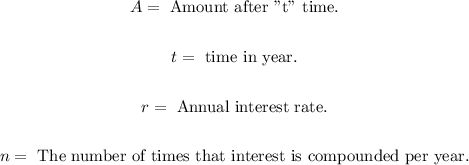
(a)
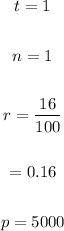
Amount after one year.
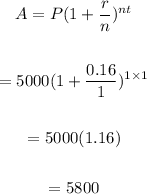
The amount after one year is $5800.
(b)
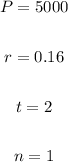
So the amount after two years is:
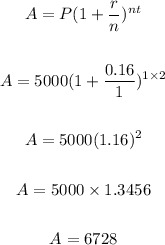
The amount after 2 years is $6728.