Question

The current (I) in a wire varies directly as the voltage (v) and inversely as the resistance (r). If the current is 27.5 amps when the voltage is 110 volts and the resistance is 4 ohms, find the current when thevoltage is 180 volts and the resistance is 12 ohms. (Round your answer to two decimal places.)

Answer 1

From the information provided in the question, we have that the current (I) varies directly as the voltage (v). This is written mathematically to be:

`I\propto v`

It is also given that the current varies inversely as the resistance (r). This is written mathematically as:

`I\propto(1)/(r)`

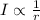
Combining both relationships, we have that:

`I\propto(v)/(r)`

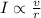
Applying a constant so that we can have an equation relating all 3 parameters, we have:

`I=(kv)/(r)`

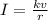
If the current is 27.5 amps when the voltage is 110 volts and the resistance is 4 ohms, we have that:

`\begin{gathered} I=27.5 \\ v=110 \\ r=4 \end{gathered}`

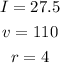
Substituting these values into the equation to get the value of the constant, we have:

`\begin{gathered} 27.5=(k*110)/(4) \\ k=(27.5*4)/(110) \\ k=1 \end{gathered}`

Therefore, the equation becomes:

`I=(v)/(r)`

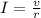
When the voltage is 180 volts and the resistance is 12 ohms, we can get the current by making the following substitution into the equation above and solving as follows:

`\begin{gathered} v=180 \\ r=12 \\ \therefore \\ I=(180)/(12) \\ I=15 \end{gathered}`

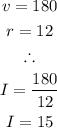
The current is 15.00 amps.