Question

using the table below find the probability express your answer as a percent to the nearest whole number sport. hikeing. reading phoningFemale 39. 48. 85. 62. male. 67. 58. 76. 54p(hiking I female)=???

Answer 1

You have to calculate the probability of the person liking hiking, given that is a female.

This a conditional probability, there are two ways of calculating it, one is using the definition of the conditional probability that states that:

"Given two dependent events A and B, the probability of A given B is equal to the probability of A and B divided by the probability of B"

`P(A|B)=(P(A\cap B))/(P(B))`

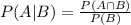
Using this option we will work using all the sampled people.

The second option, considering that we already know the person is "female" is to work directly with the group of females and calculate the probability of hiking.

Let "H" represent the event "hiking" and "F" represent the event "female"

1) Using the definition of conditional probability.

`P(H|F)=(P(H\cap F))/(P(F))`

First lets determine the probability of "female", to do so you have to divide the number of females by the total number of people on the sample:

Total females:

`F=39+48+85+62=234`

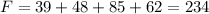
Total number of people

`T=M+F=(67+58+76+54)+234=489`

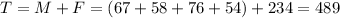
The probability of "female" is then:

`\begin{gathered} P(F)=(234)/(489) \\ P(F)=(78)/(163) \end{gathered}`

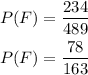
Second, calculate the probability of the intersection between "female" and "hiking". For this calculateion you have to divide the number of people that are females and like hiking, by the total number of people

`\begin{gathered} P(H\cap F)=(48)/(489) \\ P(H\cap F)=(16)/(163) \end{gathered}`

Now you can calculate the conditional probability as:

`\begin{gathered} P(H|F)=(P(H\cap F))/(P(F)) \\ P(H|F)=((16)/(163))/((78)/(163))=(16)/(163)\cdot(163)/(78) \\ P(H|F)=(8)/(39) \end{gathered}`

2) The second option was to work only with the data of the "female" group.

To calculate the probability of the person liking hiking, given that she is female, you have to divide the total number of females that like hiking by the total number of females of the sample

`\begin{gathered} P(H|F)=(48)/(234) \\ P(H|F)=(8)/(39) \end{gathered}`

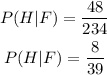
Using both ways, we reached the same result, the probability of P(H|F)=8/39

As a percentage is (8/39)*100=20.51%