Question

How many seconds are required for the ranger’s vehicle in the previous problem to stop? Only enter the number not the units

Answer 1

distance = 17.1 m

time = 3 s

Step-by-step explanation:

First, we will use the following equation:

`v^2_f=v^2_i+2a(\Delta x)`

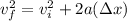
Where vf is the final velocity, vi is the initial velocity, a is the acceleration and

Δx is the distance. Then, replacing each value, we get:

`\begin{gathered} 0^2=11.4^2+2(-3.8)(\Delta x) \\ 0=129.96-7.6\Delta x \end{gathered}`

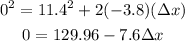
The final velocity is 0 m/s because the vehicle will come to rest and the acceleration is negative because it is slowing down.

Then, solving for Δx, we get:

`\begin{gathered} 7.6\Delta x=129.96 \\ (7.6\Delta x)/(7.6)=(129.96)/(7.6) \\ \Delta x=17.1\text{ m} \end{gathered}`

Now, with the distance and velocities, we can find the time t using the following equation:

`\Delta x=(1)/(2)(v_i+v_f)t`

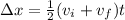
So, replacing the values and solving for t, we get:

`\begin{gathered} 17.1=(1)/(2)(11.4+0)t \\ 17.1=(1)/(2)(11.4)t \\ 17.1=5.7t \\ (17.1)/(5.7)=(5.7t)/(5.7) \\ 3\text{ s = t} \end{gathered}`

Therefore, the answers are:

distance = 17.1 m

time = 3 s