Question

An object s 12 cm in front of a convex lens focal length of 6 cm. The characteristics of the image are___.a. real inverted at a distance of 12 cmb. virtual, upright at a distance of 2.4cmc. real, upright at a distance of 4 cm d. virtual, inverted at a distance of 6 cmMust follow GRESA formatGIVEN:REQUIRED:EQUATION(S) NEEDED:SOLUTION:FINAL ANSWER:L-ocation:O-rientation:S-ize:T-ype

Answer 1

Given data:

* The focal length of the convex lens is f = 6 cm.

* The distance of the object is u = 12 cm.

Required: The nature of the image formed.

Equations needed:

The lens formula:

`(1)/(v)-(1)/(u)=(1)/(f)`

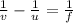
The magnification formula:

`m=(v)/(u)=(h_i)/(h_o)`

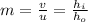
Solution:

The radius of curvature of a convex lens is,

`\begin{gathered} R=2f \\ R=2*6 \\ R=12\text{ cm} \end{gathered}`

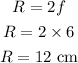
By the lens formula,

`\begin{gathered} (1)/(f)=(1)/(v)-(1)/(u) \\ (1)/(6)=(1)/(v)-(1)/((-12))_{} \\ (1)/(6)=(1)/(v)+(1)/(12) \\ (1)/(v)=(1)/(6)-(1)/(12) \end{gathered}`

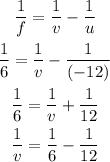
By simplifying,

`\begin{gathered} (1)/(v)=(2-1)/(12) \\ (1)/(v)=(1)/(12) \\ v=12\text{ cm} \end{gathered}`

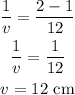
The positive value of image distance indicated that the real image is formed.

The magnification of the image is,

`\begin{gathered} m=(v)/(u) \\ m=(12)/(-12) \\ m=(-12)/(12) \\ m=-1 \end{gathered}`

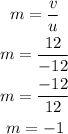
The value of magnification indicates that the size of the image is the same as the size of the object.

The negative sign with the magnification indicates that the inverted image is formed.

Final Answer:

Location - 12 cm (Center of curvature)

Orientation - Inerted

Size - Same as an object

Type - Real

Hence, option a is the correct answer.