Given:
• First term, a1 = 19
,
• an = 309
,
• number of terms, n = 30
Let's find the sum of the sequence.
To find the sum of an arithmetic sequence, apply the formula:
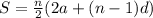
Where d is the common difference.
To find the common difference, d, apply the explicit formula of an arithmetic sequence:
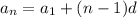
Plug in the values and solve for d:

Divide both sides by 29:
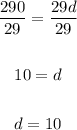
The common difference, d = 10.
Now, plug in values on the sum formula and solve for the sum, S.
We have:
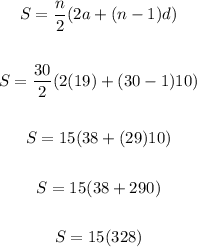
Solving further:
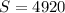
Therefore, the sum of the sequence is 4920.
• ANSWER:
4920