Question

The sum of two numbers is 60. The larger number is 6 more than the smaller number. What are the numbers.Larger number:Smaller numbers:

Answer 1

Let the smaller number be 'x' and the larger number be 'y'.

Given that the sum of the numbers is 60,

`\begin{gathered} x+y=60 \\ y=60-x \end{gathered}`

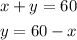
Also, given that the larger number is 6 more than the smaller number,

`y=x+6`

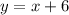
Substitute the value,

`x+6=60-x`

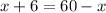
Taking the variables and constants on either side,

`\begin{gathered} x+x=60-6 \\ 2x=54 \end{gathered}`

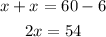
Divide both sides by 2,

`\begin{gathered} (2x)/(2)=(54)/(2) \\ x=27 \end{gathered}`

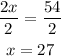
Substitute this value and obtain the other variable,

`\begin{gathered} y=60-27 \\ y=33 \end{gathered}`

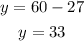
Thus, the larger number is 33 and the smaller number is 27.