This problem can be seen as the next equation
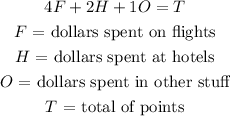
Since he have charged 9480 dollars in total then we also have the next equation.
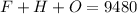
With the rest of the information, we conclude the next system of equations
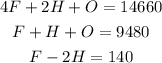
From the first two equations, we can substract them to obtain
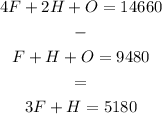
If we multiply this last equation by 2 and add it to the last equation in the system we have
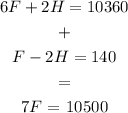
So
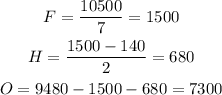
Then, he spent 1500 dlls. on flights, 680 dlls. at hotels and 7300 dlls. on others
