Question

1) What are the values of a and b for each equation? Why does this represent exponential growth? 3) Compare and contrast the value of y as x increases. Equation a value b value y= (1) y--(3) r 2) What will be the y-intercept for each graph? 4) What transformations does this represent?

Answer 1

1) If we express an exponential function as y=a^bx, we can identify the coefficients from the following functions:

`y=((1)/(3))^x\longrightarrow a=(1)/(3),b=1`
`y=-((1)/(3))^x\longrightarrow a=(1)/(3),b=1`

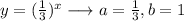
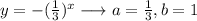
In the second function, we have a -1 multiplying the function, but the base coefficient is a=1/3 and the exponent coefficient is b=1, the same as the first function.

2) The y-intercept is the value of y when x=0. We can calculate them as:

`y(0)=((1)/(3))^0=1`
`y(0)=-((1)/(3))^0=-1`

The y-intercept is 1 for the first function and -1 for the second function.

3) For the first function, the value of y decreases as x increases as we have a coefficient a that is smaller than 1. Then, as x increases, powers of values that are smaller than 1 become smaller.

In the case of the second function, the value of y increases when x increases as the negative value reduces. That is: it approaches to 0 as x increases, but as we start with negative values, it is an increase in the value of y.

4) If we relate the first function with the second one with a transformation, they are the reflection of each other in the x-axis:

`(x,y)\longrightarrow(x,-y)`