Quadratic equations can have two solutions, then, we can build one whose 2 solutions are 12 and 116.
It can be built as follows:
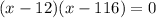
The equation is a product of two expressions equal to 0. When a product is 0, we know that either the first parenthesis or the second one is equal to 0. Then, the solution x for the above equation can be:
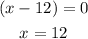
Or well:
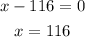
Both 12 and 116 solve the equation. We can rewrite the equation by solving the multiplication:
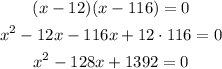
Then, an equation that has as solutions both 12 and 116 could be:
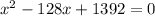
If we plug either value on the x of the equation we will see that the equality is fulfilled. Alternatively, if we solve the quadratic equation with the general formula, we will also obtain that the x can take the values of both 12 and 116