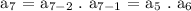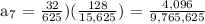Given:
a₁ = 2/5
a₂ = 4/5
Since the first 2 terms are given, let's determine the remaining 3 terms using the given formula:

We get,
For a₃,
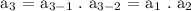
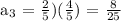
For a₄,
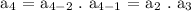
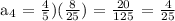
For a₅,
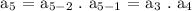
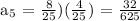
Therefore, the first five terms of the sequence are the following:
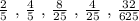
For another two terms.
For a₆,
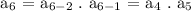
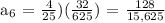
For a₇,