Question

create 2 linear equations, in the form y=mx+b-the two lines are perpendicular to each other and both lines pass through the point (3,-5)

Answer 1

`\begin{gathered} y=x-8 \\ y=-x-2 \end{gathered}`

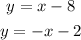
Step-by-step explanation

Step 1

two lines are perpendicular if the producto of their slopes equals -1

so

`\begin{gathered} so\mathrm{}\text{let} \\ \text{slope}1|\cdot\text{solpe}2=-1 \\ \text{slope}1=1 \\ \text{slope}2=-1 \end{gathered}`

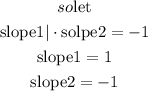
Step 2

now, find the equations

a) for line 1

Let

slope=1

point (3,-5)

to find the equation ,let's use the formula

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{replace} \\ y-(-5)=1(x-3) \\ y+5=x-3 \\ \text{subtract 5 in both sides} \\ y+5-5=x-3-5 \\ y=x-8 \end{gathered}`

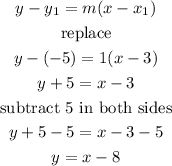
therefore, the equation 1 is

`y=x-8`

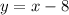
b) for line 2

let

slope=slope2=-1

point=(3,-5)

replace in the formula

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-5)=-1(x-3) \\ y+5=-x+3 \\ \text{subtract 5 in both sides} \\ y+5-5=-x+3-5 \\ y=-x-2 \end{gathered}`

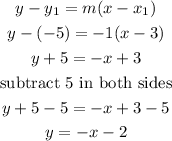
, therefore, the equations are

`\begin{gathered} y=x-8 \\ y=-x-2 \end{gathered}`

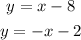
I hope this helps you