We have a quadrilateral given by the following vertices:
• E = (1, -4),
,
• F = (10, -4),
,
• G = (10, 0),
,
• H = (1,0).
A rotation of the coordinates of the vertices in 270° counterclockwise around the origin, is equivalent to the following transformation of the coordinates:
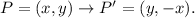
Applying this transformation to the points above, we get:
• E' = (-4,-1),
,
• F' = (-4,-10),
,
• G' = (0,-10),
,
• H' = (0,-1).
Answer
• E' = (-4,-1),
,
• F' = (-4,-10),
,
• G' = (0,-10),
,
• H' = (0,-1).
Verification