Question

Solve the following system of equations. (Hint: Use the quadratic formula.) f(x) = 2x² 3x g(x)=-3x² + 20 (0.-10) and (1, 17) (-2.2, 5.9) and (3.2, 0.9) (28.-3.0) and (-1.5, -1) (-2.2, 5.9) and (2.8, -3,0)

Answer 1

The solution of the system of equation is the intersection point of the two quadratic equations, so we need to equate both equations, that is,

`2x^2-3x-10=-3x^2+20`

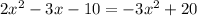
So, by moving the term -3x^3+20 to the left hand side, we have

`5x^2-3x-30=0`

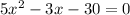
Then, in order to solve this equation, we can apply the quadratic formula

`x=(-b\pm√(b^2-4ac))/(2a)`

In our case, a=5, b=-3 and c=-30. So we get

`x=(3\pm√((-3)^2-4(5)(-30)))/(2(5))`

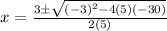
which gives

`\begin{gathered} x=2.76779 \\ and \\ x=-2.16779 \end{gathered}`

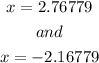
By substituting these points into one of the functions, we have

`f(2.76779)=-2.982`

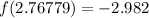
and

`f(-2.16779)=5.902`

Then, by rounding these numbers to the nearest tenth, we have the following points:

`\begin{gathered} (2.8,-3.0) \\ and \\ (-2.2,5.9) \end{gathered}`

Therefore, the answer is the last option