Question

Use the equation to find: where he is after 12 seconds

Answer 1

After 12 seconds, he is 36 meters behind the start line

Step-by-step explanation

We know that Charlie has a 12 m head start so, if y is the distance and x is the time in seconds, and he runs the opposite direction at 4 meters per second, then each second he moves back 4 meters. The recursive rule for the distance, y, is,

`y_n=y_(n-1)-4`

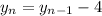
Where n is the seconds after the race started. This way, in the first second he is 4 meters before his starting point, so he is 8 meters from the start line, then 2 seconds after the beginning of the race, he is 4 meters from the start line, and so on.

The equation is the head start of 12 meters minus 4 times x. This equation will give us Charlie's position each second,

`y=12-4x`

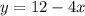
Using this equation, we can complete the table,

Using the equation or the table we can draw the graph, which is a line. To do so, use the vertical axis for y and the horizontal axis for x. Place a point at y = 12 on the y-axis, since this is when x = 0. Then the values become negative after a while, so we can draw the horizontal axis in the upper half of the provided grid to obtain negative values. Draw the second point of the table, (5, -8) and join those two points with a line,

Now, finally, we have to use the equation to find where is Charlie after 12 seconds. In other words, we have to substitute x with 12 in the equation we found before and solve it to find y,

`y=12-4x=12-4\cdot12=12-48=-36`

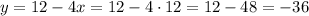
Hence, after 12 seconds, Charlie is 36 meters behind the start line.