Given:
Given the data set
6, 6, 6, 7, 8, 9, 9, 10, 11, 12, 12, 13, 14, 15, 18
Required: Interquartile range
Explanation:
Sample size is n = 15.
First, arrange the data set in ascending order.
6, 6, 6, 7, 8, 9, 9, 10, 11, 12, 12, 13, 14, 15, 18
Compute the quartiles Q1 and Q3.
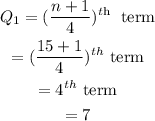
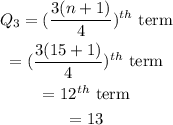
The interquartile range is
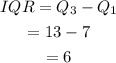
Final Answer: The interquartile range of the given data set is 6.