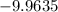Question

I believe the answer to be this: but I'm not too sure-99.2016I'm not understanding what it mean by win or lose I don't know which one to mark

Answer 1

Hello there. To solve this question, we'll have to remember some properties about probabilities.

First, remember that there are 4 suits in a standard card deck, each containing 13 different cards.

Most specifically, there are only one of each number in each suit, so this means that there are only 4 cards with the number 5 in a 52 card deck.

The probability of taking three fives in succession from this deck, with replacement, is given by the ratio between the favorable events of taking a 5 (4) and the total number of cards (52), cubed:

`P(\text{taking a 5 three times in succession)}=(4)/(52)\cdot(4)/(52)\cdot(4)/(52)=(1)/(13^3)=(1)/(2197)`

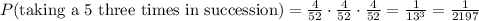
Notice the probabilities are the same for each succession because we were replacing the cards. If we weren't replacing, then the probabilites would go down as 4/52 * 3/51 * 2/50, which is not the case.

Obviously, this is the probability of winning and if you get three fives in succesion, you get $70.

To find the probability of not getting 5's three times in succession, simply subtract the probability we found from 1:

`P(\text{not get 5's three times in succession)}=1-(1)/(2197)=(2196)/(2197)`

Now, we multiply the probabilities by the number in dollars we would get by winning and the number in dollars (negative) we would pay for losing, respectively:

`\begin{gathered} 70\cdot(1)/(2197)-10\cdot(2196)/(2197) \\ \\ (70)/(2197)-(21960)/(2197) \\ \\ -(21890)/(2197) \end{gathered}`

By calculating the fraction, we get:

`-9.9635`