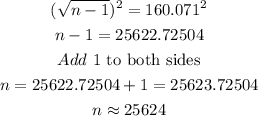Question

You want to obtain a sample to estimate how much parents spend on their kids birthday parties. Based on previous study, you believe the population standard deviation is approximately σ=68.7 dollars. You would like to be 98% confident that your estimate is within 1 dollar(s) of average spending on the birthday parties. How many moms do you have to sample? Do not round mid-calculation.n = 25535

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given parameters

`\begin{gathered} \sigma=68.7 \\ C.I=98\% \\ n=? \end{gathered}`

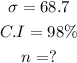
STEP 2: Get the z-score for the given Confidence interval

98% confidence is equivalent to 2.33 standard deviations. So you want $1 = 2.33 σ. That tells us the standard deviation of the sample mean needs to be:

`(1)/(2.33)=0.429184549`

The standard deviation of the sample mean is equal to:

`(68.7)/(√(n-1))`

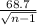
This implies that:

`(68.7)/(√(n-1))=0.429184549`

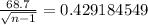
STEP 3: Solve the equation for n

`\begin{gathered} (68.7)/(√(n-1))=0.429184549 \\ √(n-1)=(68.7)/(0.429184549) \\ \\ √(n-1)=160.071 \end{gathered}`

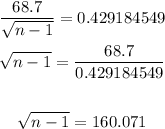
Find the square of both sides:

`\begin{gathered} (√(n-1))^2=160.071^2 \\ n-1=25622.72504 \\ Add\text{ 1 to both sides} \\ n=25622.72504+1=25623.72504 \\ n\approx25624 \end{gathered}`