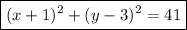The Equation of a Circle
If a circle has its center at the point (h, k) and has a radius r, the equation of the circle is:

We are only given the endpoints of the diameter of the circle (3, -2) and (-5, 8). We need to find its center and radius.
These facts will help us to find both parameters:
* The diameter passes through the center of the circle.
* The center of the circle is the midpoint of the diameter.
* The radius of the circle is half the length of the diameter.
The midpoint of the diameter can be calculated as:


The coordinates of the midpoint are (-1, 3) and it happens to be the center of the circle, thus h = -1 and k = 3.
To find the radius, we need to calculate the distance from the center to any of the endpoints. Let's use the points (-1, 3) and (3, -2) and use the formula of the distance:
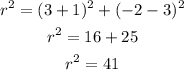
We don't need to calculate the value of r. Its square is enough to substitute in the general form of the circle to get: