Question

Accurately sketch or graph: f(x) = x^4/4 - 2x^3/3 -x^2/2 + 2xon the interval [ -2.5, 2.3] using the graph paper provided.

Answer 1

`\begin{gathered} \text{ Given} \\ f\mleft(x\mright)=(x^4)/(4)-(2x^3)/(3)-(x^2)/(2)+2x \end{gathered}`

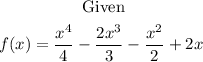
Graphing the function f(x) over the interval [-2.5, 2.3], we have the following

x-intercepts

Judging on the graph, the x-intercept of the function f(x) are the following

`x=-1.619\text{ and }x=0`

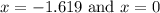
critical points

Finding the first derivative and setting it to zero and solve for x to get the critical points in the interval [-2.5,2.3] we have

`\begin{gathered} f\mleft(x\mright)=(x^4)/(4)-(2x^3)/(3)-(x^2)/(2)+2x \\ f^(\prime)\left(x\right)=x^3-2x^2-x+2 \\ \\ x^3-2x^2-x+2=0 \\ \left(x−2\right)\left(x+1\right)\left(x−1\right)=0 \end{gathered}`

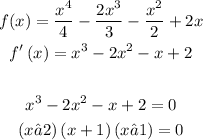
Therefore, the critical points are x = 2, x = 1, x = -1.

relative minimums

Basing on the graph our relative minimum is at x = -1, and x = 2

asymptotes

Since the given function is a polynomial function, the function has no asymptotes

critical numbers

same as critical points with x = 2, x = 1, and x = -1.

relative maximum

observing the graph, the relative maximum of the function is at x = 1.

inflection points

get the second derivative of the function and set it to zero

`\begin{gathered} f^(\prime)\left(x\right)=x^3-2x^2-x+2 \\ f^(\prime)^(\prime)\left(x\right)=3x^2-4x-1 \\ 3x^2-4x-1=0 \end{gathered}`

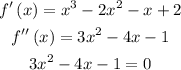
Using the quadratic formula we have the values at

`x=(2)/(3)\pm\sqrt{(7)/(3)}`

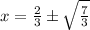
end behavior

Since the function is a polynomial with a degree of 4, and a positive leading coefficient, the end behavior of the function is increasing in both approaching to -2.5, and 2.3.