Question

Solve for x and graph the solution on the number line below. If possible, resolve your answer to a single inequality. In case of no solution (∅), leave the number line blank.34<3x+7 and 43>3x+7

Answer 1

So,

Here we have the following inequalities:

`34<3x+7\text{ and }43>3x+7`

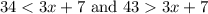
We're going to solve each inequality and then notice which could be the solution set.

Let's begin with:

Now, what we have to do is to graph both solution sets and find the intersection between them:

As you can notice, both solution sets intersect at the interval (9,12).

So, the solution set is (9,12), which is: 9

If you have to graph it, put:

Which is 9