Question

6.In physical education class, Ariel shoots free throws and lay-ups. She earns 1 point for eachfree throw she makes and 2 points for each lay-up she makes. The greatest number of pointsthat she can earn is 30. She has to make at least 15 free throws and lay-ups altogether.a. Write a system of inequalities (two inequalities) to describe the constraints.Specify what each variable represents. (4pts)Ib. Name one possible solution to the system of inequalities and explain what itrepresents in that situation. (4pts)

Answer 1

Let's call t the free throw and l the lay-up.

We know that the minimum free throws and lay-ups together must be 15, this means:

`t+l\ge15`

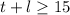
We also know that the maximum points to earn it 30. Because each t earns 1 point and each l earns 2 points, we can right:

`\begin{gathered} 1\cdot t+2\cdot l\le30 \\ t+2l\le30 \end{gathered}`

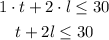
So, the system of inequalities is:

`\begin{gathered} t+l\ge15_{} \\ t+2l\le30 \end{gathered}`

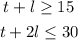
One possible solution is to make the inequalities two equalities and solve the system:

`\begin{gathered} t+l=15 \\ t+2l=30 \end{gathered}`

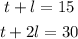
To solve, we can substract the first quation from the second:

`\begin{gathered} (t+2l)-(t+l)=(30)-(15) \\ t+2l-t-l=30-15 \\ t-t+2l-l=15 \\ l=15 \end{gathered}`
`\begin{gathered} t+l=15 \\ t+15=15 \\ t=15-15 \\ t=0 \end{gathered}`

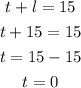
So, one possible solution is l=15 and t=0, this means that Ariel shoot 15 lay-ups and no free throws, which earns her 30 points.