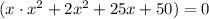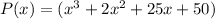Question

Find the polynomial function of lowest degree having zeros -2 and 5i

Answer 1

`P(x)=(x^(3)+2x^(2)+25x+50)`

Step-by-step explanation

Given

• Polynomial function of lowest degree

,

• Zeros -2 and 5i

Procedure

The zeros of the polynomial can be written as

`\begin{gathered} x=-2 \\ x+2=0 \end{gathered}`
`\begin{gathered} x=5i \\ x-5i=0 \end{gathered}`
`\begin{gathered} x=-5i \\ x+5i=0 \end{gathered}`

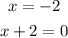
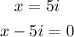
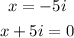
If we multiply each other we get:

`(x+2)(x-5i)(x+5i)=0`

Multiplying the last two factors is the sum of two squares:

`(x+2)(x^2+25)=0`

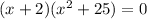
Finally, combining the terms and simplifying:

`(x\cdot x^2+2x^2+25x+50)=0`
`(x^3+2x^2+25x+50)=0`
`P(x)=(x^3+2x^2+25x+50)`