Answer:(a) dependent events (b)
P(all three cards 5 ) = 1/5525Explanation :
Part (a)
• We are told that cards are drawn without replacement , meaning the drawing of one card at a time will affect the occurence of the other card .
,
• Therefore , ,these events are dependent
Part (b)
• Take note that the deck of cards has 52 cards
,
• There are 4 cards of number 5 in the deck out of 52 cards
• Probability of first card to be a 5 , is represented as
P (first card 5) = 4/52 , then
P( second card 5 ) = 3/51 , and
P(third card 5 ) = 2/50
So, the probability of drawing three fives in a row from a standard deck of cards when the drawn card is not returned to the deck each time will be :
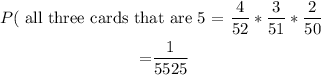
Therefore , P(all three cards 5 ) = 1/5525