Question

A farmer has 300 ft of fencing and wants to enclose a rectangular area of 5000 ft². What dimensions should she use?

Answer 1

Given:

The perimeter is 300ft.

The area of the rectangular field is 5000 square ft.

To find:

The dimensions.

Step-by-step explanation:

Using the perimeter and area formula of the rectangle,

`\begin{gathered} 2(l+b)=300............(1) \\ lb=5000..........(2) \end{gathered}`

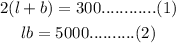
From (1),

`\begin{gathered} 2(l+b)=300 \\ l+b=150 \\ l=150-b.........(3) \end{gathered}`

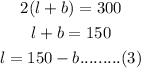
Substituting (3) in (2) we get,

`\begin{gathered} (150-b)b=5000 \\ 150b-b^2=5000 \\ b^2-150b+5000=0 \\ b^2-100b-50b+5000=0 \\ b(b-100)-50(b-100)=0 \\ (b-50)(b-100)=0 \\ b=50,100 \end{gathered}`

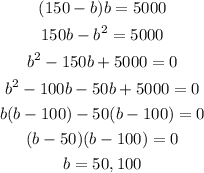
Substituting b =50 in equation (3), we get

`\begin{gathered} l=150-50 \\ l=100 \end{gathered}`

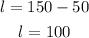
Substituting b =100 in equation (3), we get

`\begin{gathered} l=100-50 \\ l=50 \end{gathered}`

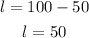
So, the dimensions are,

If the length is 100ft, then the width is 50 ft.

If the length is 50ft, then the length is 100ft.

Final answer:

The dimensions are,

• If the length is 100ft, then the width is 50 ft.

,

• If the length is 50ft, then the width is 100ft.