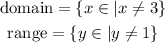Graph the function State the domain and range f(x) = (2)/(x - 3) + 1

Question

Graph the function State the domain and range
`f(x) = (2)/(x - 3) + 1`

Answer 1

In general, given a function g(x), a vertical shift is given by the transformation below

`\begin{gathered} g(x)\to g(x)+b \\ b>0\to\text{ upwards translation} \\ b<0\to\text{ downwards translation} \end{gathered}`

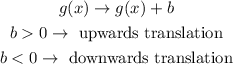
Therefore, f(x) is the graph of 2/(x-3) translated 1 unit upwards.

Notice that 2/(x-3) is a rational function; then, we need to find its asymptotes as shown below

`\begin{gathered} (2)/(x-3)\to\text{ un}\det er\min ed\text{ when x-3=0} \\ x-3=0 \\ \Rightarrow x=3 \\ \Rightarrow\text{vertical asymptote: }x=3 \end{gathered}`

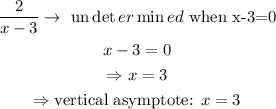
As for the horizontal asymptote,

`\begin{gathered} \frac{2\to\text{ degree zero}^{}}{x-3\to\text{ degre}e\text{ one}} \\ \text{degre}e\text{ of denominator>degre}e\text{ of numerator} \\ \Rightarrow y=0\to\text{ horizontal asymptote.} \end{gathered}`

However, we need to translate the graph upwards by one unit; then, the horizontal asymptote becomes y=1.

Knowing the asymptotes, we can graph the function, as shown below

In more detail

Finally, as for the domain and range of the function, the asymptotic values are not included; therefore,

`\begin{gathered} \text{domain}=\mleft\lbrace x\in\R|x\\e3\mright\rbrace \\ \text{range}=\mleft\lbrace y\in\R|y\\e1\mright\rbrace \end{gathered}`