Question

A bell with a fundamental frequency of 880 Hz is moving toward an observer at 3.5 m/s. If the speed of sound is 343 m/s, what pitch would be heard by the observer?1) 871 Hz2) 889 Hz3) 880 Hz4) 884 Hz

Answer 1

Given,

The fundamental frequency of the bell, f=880 Hz

The speed of the bell, v₀=3.5 m/s

The speed of the sound, v=343 m/s

The pitch heard by the observer due to the doppler shift is given by,

`f_0=(f)/(1-(v_0)/(v))`

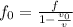
On substituting the known values,

`\begin{gathered} f_0=(880)/(1-(3.5)/(343)) \\ \approx889\text{ Hz} \end{gathered}`

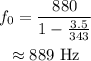
Thus the frequency heard by the observer is 889 Hz.

Therefore the correct answer is option 2.