a) Given the equation below
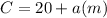
Where
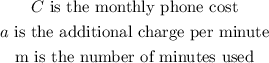
The equation that can be utilized to find the number of minutes used by a customer can be represented by making m the subject
The equation can be deduced below
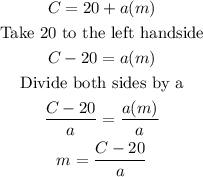
Hence, the equation to find the number of minutes, m, a customer used is
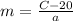
The answer is option A
b) If Alicia pays $30 and used 500 minutes, to find the additional charges
That is
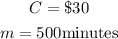
Substitute the values to find a

Where 100 cents = 1 dollar
The additional charges, a = $0.02 in cents will be
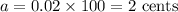
Hence, the additional charges, a, per minute used is 2 cents