We are asked to determine the amount of money if a certain amount is compounded annually. We will use the following formula:
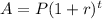
Where:
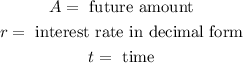
The decimal form of the interest rate is the following:
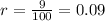
Now we substitute the given values in the formula:
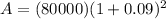
Now we solve the operations:
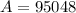
Therefore, after two years the amount is $95048.